费米网发现量子相变的扩展

事实证明，基于人工神经网络(ANN)的架构在研究环境中非常有用，因为它们可以快速分析大量数据并做出准确的预测。2020 年，谷歌的英国人工智能子公司 DeepMind 使用一种名为费米子神经网络 (FermiNet) 的新 ANN 架构来解决分子中电子的薛定谔方程，这是化学领域的核心问题。

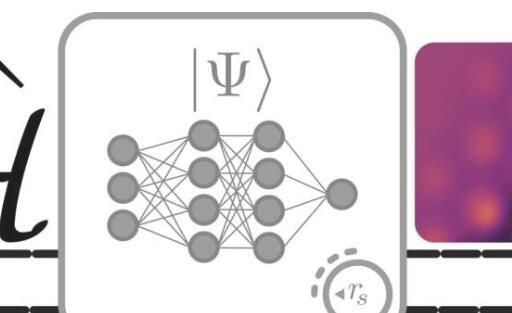
薛定谔方程是基于成熟的能量守恒理论的偏微分方程，可用于推导出有关电子行为的信息并解决与物质性质相关的问题。使用费米网(FermiNet)这是一种概念上简单的方法，DeepMind可以在化学的背景下求解这个方程，获得非常准确的结果，与使用高度复杂的量子化学技术获得的结果相当。

伦敦帝国理工学院，DeepMind，兰开斯特大学和牛津大学的研究人员最近采用了FermiNet架构来解决量子物理问题。在他们发表在《物理评论快报》上的论文中，他们专门使用费米网来计算周期性哈密顿算符的基态，并研究均匀电子气体(HEG)，这是一种电子在固体中相互作用的简化量子力学模型。

“分子很好，但物理学家更关心的是解决固体物质的薛定谔方程，”进行这项研究的研究人员之一吉诺卡塞拉告诉 Phys.org。“'凝聚态物理学'领域的核心是计算固体材料中电子的行为，从桌子的木材到为手机供电的晶体管内的硅。当然，我们很想知道费米网是否能对固体的薛定谔方程产生同样准确的解。

最初，Cassella和他的同事开始研究HEG模型。与真正的固体相比，这种简化的固体模型不包含原子，而只是在涂抹的带正电背景上呼啸而过的电子，有时被称为“jellium”(即，唤起嵌入带正电果冻中的电子的图像)。

“尽管它很简单，但HEG展示了凝聚态物理学研究中最重要的现象之一：量子相变，称为维格纳跃迁，”卡塞拉解释说。“随着HEG密度的降低，它经历了从'气体'状态到'结晶'状态的转变。我们想用维格纳跃迁两侧的费米网求解薛定谔方程，看看我们得到的解与当前最先进的方法相比有多准确。

物理研究中使用的大多数深度学习方法都依赖于对大量数据的分析，但费米网没有。相比之下，它利用了量子力学的“变分原理”，该原理指出，给定系统中波函数的猜测能量总是等于或大于所谓的“基态波函数”的能量，并且只有在猜测与基态波函数完全相同时才相等。

“这种基态波函数及其相应的能量正是我们正在寻找的解决方案，”卡塞拉说。“这意味着我们可以将能量用作我们想要尽可能低的目标函数，这就是机器学习从业者所说的'损失函数'。从本质上讲，我们仅由量子力学的基本原理指导来训练神经网络。

研究人员使用的神经网络与DeepMind应用于分子研究的原始FermiNet非常相似。与以前的版本相比，它的主要区别在于它读取系统中电子坐标的方式，必须对其进行修改以解释哈密顿算符的周期性。研究人员发现，除了为薛定谔方程提供高度精确的解外，费米网还比研究固体的传统方法具有独特的优势。

“使用现有的方法来解决薛定谔方程，人们需要提前知道波函数的一些定性特性，”卡塞拉说。“如果你期望一个'气体'波函数，你需要使用'气体'函数来设置你的计算——想象一下，通过将许多非常模糊的函数加在一起来表示波函数。同样，如果你期望一个具有许多局部峰值的'晶体'波函数，你需要使用局部函数来设置你的计算。

将一个非常本地化的波函数写成大部分被涂抹的函数之和将需要大量的计算资源和较长的处理时间。因此，为了在合理的时间内执行所需的计算，研究人员需要选择正确的函数。

“这是研究相变的一个问题，因为现在你需要改变你在过渡两侧所做的计算，”卡塞拉说。“更糟糕的是，如果你不知道过渡甚至存在怎么办?如果您选择了错误的函数集，您可能会完全错过它。这就是我们意识到费米网可以来拯救的地方。

与传统的基于计算的求解薛定谔方程的方法相比，神经网络不需要用户选择一组函数。因此，Cassella及其同事使用的FermiNet的改编版本可以获得相变两侧薛定谔方程的精确解。

“我们用完全相同的计算正确地获得了'气体'状态和'结晶'状态，只改变了HEG的密度，”Cassella解释说。“这是神经网络方法解决薛定谔方程的一个独特而惊人的优势。

这组研究人员最近的研究强调了FermiNet作为经历奇异和知之甚少的相变材料的探针的巨大潜力。虽然到目前为止，他们用它来研究HEG模型，但它很快也可以应用于高温超导体和物质的奇异相互作用拓扑相中发生的相变。

“我们关于维格纳转变的结果非常有希望，但我们真正想要研究的是真实的材料，而不是简化的模型，”卡塞拉补充道。“对真实材料进行计算，我们可以与实验进行比较，这将要求我们提高计算效率，因此这将是我们前进的主要焦点。从长远来看，我们期待研究真实固体中的相变!

　　免责声明：本文由用户上传，与本网站立场无关。财经信息仅供读者参考，并不构成投资建议。投资者据此操作，风险自担。 如有侵权请联系删除！